Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Расчет площади поверхности изделия
zpromma.ru
-
- Время чтения: 1 мин
- Просмотров: 2184
Для определения площади поверхности сложной детали необходимо условно разделить ее на простые геометрические элементы. Участки изделий имеющие неправильные формы приравниваем к простым геометрическим фигурам — прямоугольнику, конусу, призме и т. д. Площадь поверхности сложной детали будет равна сумме площадей всех элементов. Далее приведены расчеты площади поверхности простых элементов, объемных фигур, а также расчеты объемов тел.
Расчет площади плоских фигур
Для расчета площади выберете фигуру из списка и подставьте измеренные значения (в мм.) в формы для ввода, отметьте необходимые вам единицы измерения площади.
Расчет площади поверхности и объема фигур
Для расчета площади поверхности и объема выберете из списка необходимую фигуру и введите измеренные значения в поля для ввода. Программа рассчитает значения в мм, см, дм или метрах (выбор значения из списка).
Применяемые обозначения:
- a, b, c — стороны фигур;
- h, h2, h3 — высоты фигур;
- D, d — наружный и внутренний диаметр;
- d1, d2, d3 — диагонали фигур;
- l — длина дуги или образующей;
- R, r — радиусы;
- n — число сторон или граней;
- m — размер на основании тела;
- Sb — боковая поверхность тела;
- Sn — полная поверхность тела;
- V — объем тела.
Добавить комментарий
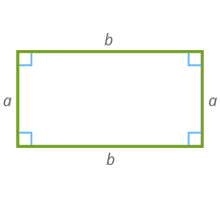
Площадь прямоугольника. Онлайн-калькулятор
Рассчитать
Прямоугольник – это геометрическая фигура, представляющая собой четырехугольник, у которого все углы прямые (90° ). Диагонали прямоугольника равны между собой.
Как найти площадь прямоугольника?
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
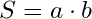a, b – стороны
2) через диагонали и угол
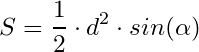d – диагонали, α – угол между диагоналями.
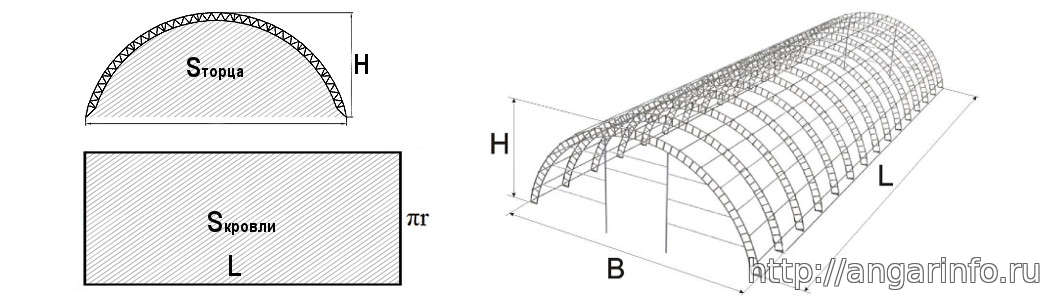
При строительстве ангаров из металлоконструкций часто встает вопрос о том, как правильно рассчитать площадь кровельного покрытия для закупки материалов. Если расчет двускатной крыши не вызывает особых сложностей, то с расчетом кровли арочного ангара у многих возникают трудности. В данной статье мы рассмотрим как правильно рассчитать площадь поверхности арочного ангара.
Мы работаем по всей России. Оставьте заявку на расчет стоимости ангара на нашем сайте, сравните сметы разных компаний и выберите лучшее предложение.
На самом деле здесь тоже ни чего сложного нет, просто надо вспомнить школьный курс геометрии. По сути, нам необходимо рассчитать площадь поверхности половины цилиндра.
Как мы помним и школьного курса геометрии, площадь боковой поверхности цилиндра рассчитывается по формуле: S=2πRh, площадь основания цилиндра: S=πR2, а общая площадь поверхности цилиндра: S=2πR(R+h), где
π – 3,14,
R – радиус цилиндра
h – высота цилиндра
Расчет площади арочного ангара
В нашем случае площадь поверхности арочного ангара равна половине площади цилиндра, то есть S=πR(R+h), при условии, что ангар имеет правильную арочную форму, где высота по коньку равна половине ширины ангара, это и будет радиус.
Но если высота ангара не равна половине ширины, то есть ангар имеет вытянутую форму, например при ширине ангара в 20 метров и высоте по коньку 8 метров, то необходимо в формулу внести некоторые корректировки. Здесь математическая формула в чистом виде нам уже не поможет, так как придется иметь дело с интегралами. А нам оно зачем? Такая точность расчетов ни к чему.
Если мы возьмем за радиус половину ширины ангара, то у нас расчетная площадь получится больше фактической, что приведет к закупкам лишнего кровельного материала. Если за радиус принять высоту по коньку, то кровельного материала может не хватить. Практика показала, что в данном случае за радиус стоит принимать среднее арифметическое значение. То есть взять половину ширины ангара, в нашем случае 20/2=10м. сложить с высотой 8м. и поделить на 2. В итоге за радиус необходимо принять значение (10+8)/2=9м.
Давайте попробуем рассчитать площадь стандартного арочного ангара 1000 м2 – 20х50 метров с высотой по коньку 8 метров.
S=3,14 х 9 (9+50) = 1667,34 ≈ 1668 м2.
Расчет кровельного материала для покрытия арочного ангара
Теперь можно посчитать, сколько необходимо кровельного материала для покрытия ангара. Допустим у нас только одни торцевые ворота 4х6 метров. Если ворота тоже будут покрыты тем же материалом, то мы площадь ворот из общей площади поверхности ангара не вычитаем. Если же ворота будут изготовлены из другого материала, то их площадь можно вычесть из общей (1668-24 = 1644 м2).
Возьмем стандартный профилированный лист с рабочей шириной 1150 х 6000. Площадь одного листа = 6,9 м2. Чтобы рассчитать, сколько нам потребуется таких листов делим общую площадь поверхности ангара на площадь одного листа 1644/6,9 = 238.26. Нам потребуется 239 стандартных шестиметровых листов. Это расчет условный. Если вы планируете делать нахлест не в одну волну, а в две, то количество листов потребуется больше. Необходимо брать в расчет только рабочую поверхность листа, как по ширине, так и по длине. И не забывайте, что при покрытии торцов ангара некоторое количество листов придется обрезать по радиусу арки.
Калькулятор расчета площади кровли арочного ангара
Данный расчет произведен по условно допустимой формуле описанной в данной статье.
Если Вам необходимо произвести расчет стоимости для строительства ангара по указанным габаритам, то воспользуйтесь калькулятором внизу страницы или оставьте заявку на расчет на странице НАЙТИ ПОДРЯДЧИКА.
Возможно вас заинтересует:
Калькулятор площади поверхности
квадратная форма пирамиды
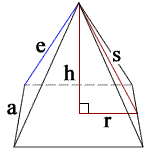
h = высота
с = наклонная высота
а = длина стороны
e = длина бокового края
р = а / 2
V = объем
S tot = общая площадь поверхности
S lat = площадь боковой поверхности
S бот = площадь нижней поверхности
Рассчитайте больше с
Пирамидальный калькулятор
Использование
Онлайн калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усечку, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферическую крышку и треугольную призму
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на расчеты.Единицы измерения установлены для указания порядка результатов, таких как футы, футы , 2 или футы , 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к V в мм 3 и к S в мм 2 .
Ниже приведены стандартные формулы для площади поверхности.
Формулы площади поверхности:
.Площадь поверхности капсулы
- Объем = № 2 ((4/3) r + a)
- Площадь поверхности = 2πr (2r + a)
Площадь поверхности круглого конуса
- Объем = (1/3) № 2 ч
- Площадь боковой поверхности = πrs = πr√ (r 2 + h 2 )
- Площадь поверхности основания = πr 2
- Общая площадь поверхности
= L + B = πrs + πr 2 = πr (s + r) = πr (r + √ (r 2 + h 2 ))Площадь поверхности круглого цилиндра
- Объем = № 2 ч
- Площадь верхней поверхности = № 2
- Площадь поверхности дна = № 2
- Общая площадь поверхности
= L + T + B = 2πrh + 2 (πr 2 ) = 2πr (h + r)Коническая площадь поверхности усеченного конуса
- Объем = (1/3) πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π (r 1 + r 2 ) с = π (r 1 + r 2 ) √ ((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = № 1 2
- Площадь поверхности основания = № 2 2
- Общая площадь поверхности
= π (r 1 2 + r 2 2 + (r 1 * r 2 ) * с)
= π [r 1 2 + r 2 2 + (r 1 * r 2 ) * √ ((r 1 — r 2 ) 2 + h 2 )]Площадь поверхности куба
- Объем = 3
- Площадь поверхности = 6a 2
Площадь полушария
- Объем = (2/3) № 3
- Площадь криволинейной поверхности = 2πr 2
- Площадь поверхности основания = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Площадь поверхности пирамиды
- Объем = (1/3) a 2 ч
- Площадь боковой поверхности = a√ ( 2 + 4 ч 2 )
- Площадь базовой поверхности = 2
- Общая площадь поверхности
= L + B = 2 + a√ ( 2 + 4 ч 2 ))
= a (a + √ ( 2 + 4 ч 2 ))
Как рассчитать площадь поверхности тела?
В зависимости от типа тела существуют разные формулы и необходимая информация. Ниже приведены формулы для расчета площади поверхности наиболее распространенных типов телосложения.
Во всех расчетах площади поверхности убедитесь, что все длины измеряются в одной единице, например дюймы, футы, мм, см.Результат нашего калькулятора площади поверхности всегда будет квадратом одной и той же единицы: квадратные футы, квадратные дюймы, квадратные метры, квадратные см, квадратные мм. и т. д.
Площадь поверхности куба
Формула площади поверхности для куба составляет 6 x сторона 2 , как показано на рисунке ниже:
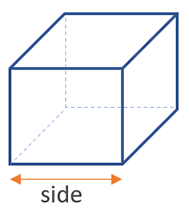
Этот расчет требует только одного измерения из-за симметричности куба. сторона 2 — это поверхность одной из сторон, и поскольку куб имеет 6 равных сторон, умножение на 6 дает нам общую площадь поверхности куба.
Площадь поверхности коробки
Формула площади поверхности для прямоугольной коробки равна 2 x (высота x ширина + ширина x длина + высота x длина) , как показано на рисунке ниже:
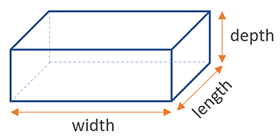
Поскольку прямоугольный ящик или резервуар имеют противоположные стороны, которые равны, мы вычисляем площадь каждой уникальной стороны, затем складываем их вместе и, наконец, умножаем на два, чтобы получить общую площадь поверхности.
Площадь поверхности цилиндра
Формула площади поверхности для цилиндра: π x диаметр x (диаметр / 2 + высота) , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому другой способ записать его — π x радиус x 2 x (радиус + высота) .Визуальный на рисунке ниже:
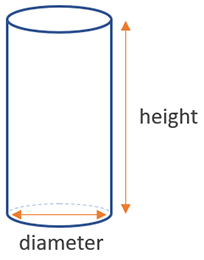
Площадь поверхности цилиндра — это высота, умноженная на периметр кругового основания, плюс площади двух оснований, сложенных вместе.
Площадь поверхности сферы
Формула площади поверхности для сферы: 4 x π x (диаметр / 2) 2 , где (диаметр / 2) — радиус сферы (d = 2 xr), поэтому можно написать еще один способ: 4 x π x радиус 2 . Визуальное изображение на рисунке ниже:
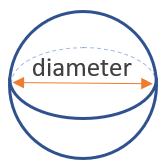
Площадь поверхности сферы можно рассчитать, просто зная ее диаметр или радиус (диаметр = 2 x радиус).π, конечно, хорошо известная математическая константа, примерно равная 3.14159.
Площадь поверхности конуса
Формула площади поверхности конуса с учетом его диаметра (или радиуса) и высоты составляет π x (диаметр / 2) 2 + π x (диаметр / 2) x √ ((диаметр / 2) 2 + (высота 2 )) , где (диаметр / 2) — это радиус основания (d = 2 xr), поэтому еще один способ записать его: π x радиус 2 + π x радиус x √ (радиус 2 + (высота 2 )) , как показано на рисунке ниже:
Площадь поверхности конуса является одной из самых сложных, и именно здесь потребность в калькуляторе становится более очевидной.Вам нужно всего два измерения: диаметр основания и его высота, но исчисление более сложное, чем у большинства других простых тел.
Площадь поверхности треугольной призмы
Формула площади поверхности для треугольной призмы составляет 2 * (высота x основание / 2) + длина x ширина 1 + длина x ширина 2 + длина x основание , как показано на рисунке ниже:
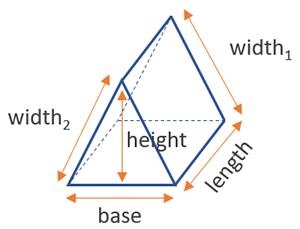
Треугольная призма — это набор треугольников, поэтому при расчете площади оснований применяются обычные правила решения треугольников.
,Площадь поверхности цилиндра с калькулятором
Площадь поверхности цилиндра с калькулятором — Math Open ReferenceОпределение: Количество квадратных единиц, необходимое для точного покрытия поверхности цилиндра. Дается по формуле:
где:π — это пи, примерно 3,142
р — радиус цилиндра
ч высота цилиндра
Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра, обратите внимание, как рассчитывается площадь.
Площадь поверхности цилиндра можно найти, разбив его на три части:
- Два круга, которые составляют концы цилиндра.
- Сторона цилиндра, которая при «развёртывании» представляет собой прямоугольник
π — это пи, примерно 3,142
r — — радиус цилиндра
ч высота цилиндра
Для детального взгляда на то, как эта формула получена, см. Вывод площади поверхности цилиндра.
единиц
Помните, что радиус и высота должны быть в одинаковых единицах — конвертировать их при необходимости. Полученная площадь будет в этих квадратных единицах. Так, например, если высота и радиус указаны в сантиметрах, то площадь будет в квадратных сантиметрах.Калькулятор
Используйте калькулятор выше, чтобы вычислить высоту, радиус или площадь поверхности цилиндра.
Введите любые два значения, и недостающее будет вычислено.Например: введите радиус и высоту и нажмите «Рассчитать». Площадь поверхности будет рассчитана.
Точно так же, если вы введете высоту и площадь, будет рассчитан радиус, необходимый для получения этой области.
Что попробовать
- На рисунке выше отрегулируйте высоту и диаметр цилиндра и обратите внимание, как рассчитывается площадь поверхности.
- Нажмите «Сброс» и «Скрыть детали». Отрегулируйте цилиндр до нового размера и рассчитайте площадь поверхности.Нажмите «показать детали», чтобы подтвердить свой ответ.
- Нажмите «Сброс». Рассчитайте, что произойдет, если вы удвоите высоту — удваивается ли площадь поверхности?
- Нажмите «Сброс». Рассчитайте, что произойдет, если вы удвоите диаметр — удвоится ли площадь поверхности?
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены