Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
через основание и высотучерез две стороны и уголпо трем сторонам (формула Герона)через радиус вписанной окружностичерез радиус описанной окружностиРассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
1) через основание и высоту
a – основание треугольника,h – высота треугольника.
2) через две стороны и угол
a, b – стороны треугольника,α – угол между сторонами.
3) По трем сторонам. Формула Герона.
a, b, с – стороны треугольника,p – полупериметр треугольника.
4) Через радиус вписанной окружности.
a, b, с – стороны треугольника,p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
a, b, с – стороны треугольника,Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
calc.by
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины
Расчет площади прямоугольника
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади треугольника
Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними
ВычислитьРезультат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади круга
Рассчитать площадь круга, если известен:
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади правильного многоугольника
Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади эллипса
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
|
r= ммсммкмфутярддюйммиля |
|
|
θ= ммсммкмфутярддюйммиля град.рад. |
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади трапеции
Способ нахождения площади трапеции: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр — 1 км2 = | 1 000 000 м2 |
| Гектар — 1 га = | 10 000 м2 |
| Ар (сотка) — 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
calc.by
Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона a
Высота h
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
Сторона a
Сторона
Угол α° между сторонами a и b
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам

Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам

Сторона a
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона

Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника по стороне и двум прилежащим углам

Сторона a
Угол β°
Угол α°
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию

Сторона a (a = b)
Сторона c
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними

Боковая сторона a (a = b)
Угол α° между боковыми сторонами
9
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними

Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной
10
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию

Основание треугольника c
Высота h
12
Площадь равностороннего треугольника по стороне

Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте

Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности

Радиус r вписанной окружности
15
Площадь равностороннего треугольника по радиусу описанной окружности

Радиус R описанной окружности
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам

Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол

Сторона c
Угол α
18
Площадь прямоугольного треугольника через катет и угол

Сторона b
Угол α
19
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Отрезок d
Отрезок e
20
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность

Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона

Полупериметр:
Сторона a
Сторона b
Сторона c
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Скачать формулы площади треугольника в виде картинки
doza.pro
Площадь треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Площадь любого треугольника можно найти, зная основание и высоту. Вся простота схемы заключается в том, что высота делит основание a на две части a1 и a2, а сам треугольник – на два прямоугольных треугольника, площадь которых получается и . Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание:
Более сложный для расчетов способ – это формула Герона, для которой необходимо знать все три стороны. Для этой формулы нужно вычислить сначала полупериметр треугольника: Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.
Следующий способ, также актуальный для любого треугольника, позволяет найти площадь треугольника через две стороны и угол между ними. Доказательство этому проистекает из формулы с высотой – проводим высоту на любую из известных сторон и через синус угла α получаем, что h=a⋅sinα . Для вычисления площади умножим половину высоты на вторую сторону.
Другой способ – найти площадь треугольника, зная 2 угла и сторону между ними. Доказательство этой формулы достаточно простое, и наглядно видно из схемы.
Опускаем из вершины третьего угла высоту на известную сторону и называем полученные отрезки x соответственно. Из прямоугольных треугольников видно, что первый отрезок x равен произведению котангенса угла α на высоту, а второй отрезок y – произведению котангенса угла β на эту же высоту. Дальше соединяем это вместе:
geleot.ru
Формулы площади треугольника
Формулы площади треугольника
Подождите пару секунд пока подгрузятся формулы
Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!
Через основание и высоту
$$S= \frac{1}{2} ah $$ \(S\) — площадь треугольника\(a\) — основание
\(h\) — высота
\(a =\) \(h =\)
Через две стороны и угол
$$S= \frac{1}{2} ab sin \alpha $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\( \alpha \) — угол между сторонами \(a\) и \(b\)
\(a =\) \(b =\) \( \alpha =\)
Формула Герона
$$S= \sqrt{p(p-a)(p-b)(p-c)} $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(c =\)
Через радиус вписанной окружности
$$S= rp $$ \(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(r =\) \(p =\)
Через радиус описанной окружности
\(S= \frac{abc}{4R} \)\(S\) — площадь треугольника
\(R\) — радиус описанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(a =\) \(b =\)
\(c =\) \(R =\)
Площадь прямоугольного треугольника
$$S= \frac{1}{2} ab $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(a =\) \(b =\)
Площадь прямоугольного треугольника
$$S= de $$ \(S\) — площадь треугольника\(d =\) \(e =\)
Формула Герона для прямоугольного треугольника
$$ S= (p-a)(p-b) $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(p =\)
Площадь равнобедренного треугольника
$$S= \frac{1}{2} a^2 sin \alpha$$ \(S\) — площадь треугольника\(a\) — сторона
\(\alpha\) — угол между боковыми сторонами
\(a =\) \( \alpha =\)
Площадь равнобедренного треугольника
\(a\) — сторона
\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(a =\) \(b =\) \( \alpha =\)
Площадь равнобедренного треугольника
$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$ \(S\) — площадь треугольника\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(b =\) \(\alpha =\)
Формула Герона для равнобедренного треугольника
a = b =Площадь равностороннего треугольника
$$S= \frac{ \sqrt{3}a^2}{4} $$ \(S\) — площадь треугольника\(a\) — сторона
\(a =\)
Площадь равностороннего треугольника
$$S= \frac{3 \sqrt{3}R^2}{4}$$ \(S\) — площадь треугольника\(R\) — радиус описанной окружности
\(R =\)
Площадь равностороннего треугольника
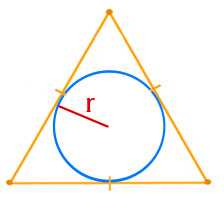 $$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника
$$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(r =\)
Площадь равностороннего треугольника
$$S= \frac{h^2}{\sqrt{3}}$$ \(S\) — площадь треугольника\(h\) — высота
\(h =\)
www.100formul.ru
Калькулятор расчета площади треугольного помещения
При расчете площадей помещений или других поверхностей, подлежащих отделке, порой приходится сталкиваться с многоугольными фигурами, которые неопытного человека могут поставить в тупик. Но на самом деле – нет ничего сложного, существует простой и точный способ провести необходимые вычисления.
 Калькулятор расчета площади треугольного помещения
Калькулятор расчета площади треугольного помещенияЛюбой многоугольник можно одной или несколькими линиями разбить на определенное количество треугольников, затем просчитать площади этих участков и просуммировать. А чтобы вычисления были произведены быстро и точно, примените предлагаемый калькулятор расчета площади треугольного помещения.
Несколько пояснений по работе с ним будут даны ниже.
Калькулятор расчета площади треугольного помещения
Перейти к расчётам
Несколько необходимых пояснений
Треугольные помещения встречаются нечасто, но калькулятор может быть полезен и в иных случаях. Как уже говорилось, на треугольники несложно разбить любую многоугольную плоскую фигуру.
 Пример разбивки неправильного четырёхугольника на два треугольника
Пример разбивки неправильного четырёхугольника на два треугольникаПлощадь треугольника чаще определяют произведением основания на высоты с последующим делением на два. Однако, в условиях стройки или ремонта пробить перпендикуляр, чтобы точно измерить высоту фигуры – не всегда бывает просто, если нет специальных инструментов. Даже небольшая ошибка в разметке способна привести к искажению конечного результата. Поэтому в данном случае применена формула Герона, позволяющая рассчитать площадь абсолютно любого треугольника по длинам трех его сторон, измерить которые – уже труда никакого не составит.
Значения запрашиваются в сантиметрах. Конечный результат – в квадратных метрах.
Если необходимо определит площадь прямоугольного или трапециевидного помещения, то есть у которого хотя бы одна пара сторон – параллельны друг другу, то для этого проще применить специальный калькулятор для четырехугольника. Он, кстати, учитывает возможное наличие выступов, колонн, ниш и других элементов, увеличивающих или уменьшающих общую площадь комнаты.
Существуют и более сложные случаи расчета площадей
Иногда приходится прибегать и к более сложным расчетам, когда некоторым стенам или элементам конструкции придана криволинейная форма. Как вычислить площадь комнаты при таких условиях – рассказывается в специальной публикации нашего портала.
stroyday.ru
Высчитать площадь треугольника в м2. Как рассчитать площадь треугольника
- Отношения
- Мода
- Красота и здоровье
- Звезды
- Дом
- Отношения
Поиск
- Мода
- Красота и здоровье
- Звезды
- Дом
- Отношения
fashion-family.ru

 Существуют и более сложные случаи расчета площадей
Существуют и более сложные случаи расчета площадей