Задачи по физике и математике с решениями и ответами
Задача по физике — 7525
Определить индукцию магнитного поля в точке О, если проводник с током $I$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника равен $R$, прямолинейные участки проводника предполагаются очень длинными.
Подробнее Задача по физике — 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба. ПодробнееЗадача по физике — 7527
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные.
Подробнее Задача по физике — 7528
Определить модуль и направление вектора $\vec{B}$ магнитного поля:а) безграничной плоскости, По которой течет ток с линейной плотностью $\vec{i}$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $\vec{i}$ и $- \vec{i}$, одинаковыми во всех точках каждой плоскости.
Задача по физике — 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства.
Подробнее Задача по физике — 7531
Имеется круговой виток с током $I$. Найти интеграл $\int \vec{B} d \vec{r}$ вдоль оси витка в пределах от $ — \infty$ до $+ \infty$. Объяснить полученный результат. ПодробнееЗадача по физике — 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $\vec{r}$. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $\vec{l}$. По проводу течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $\vec{l} = 0$.Задача по физике — 7534
Найти плотность тока как функцию расстояния $r$ от оси аксиально-симметричного параллельного потока электронов, если, индукция магнитного поля внутри потока зависит от $r$ как $B = br^{ \alpha}$, где $b$ и $\alpha$ — положительные постоянные. ПодробнееЗадача по физике — 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$. ПодробнееЗадача по физике — 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_{0}$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $\eta = 1$%. Подробнее
Задача по физике — 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси. ПодробнееЗадача по физике — 7538
На деревянный тороид малого поперечного сечения намотано равномерно $N = 2,5 \cdot 10^{3}$ витков провода, по которому течет ток $I$. Найти отношение $\eta$ индукции магнитного поля внутри тороида к индукции магнитного поля в центре тороида. ПодробнееЗадача по физике — 7539
Постоянный ток $I = 10 А$ течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины. ПодробнееЗадачи по физике и математике с решениями и ответами
Задача по физике — 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба. ПодробнееЗадача по физике — 7527
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные. Подробнее Задача по физике — 7528
Определить модуль и направление вектора $\vec{B}$ магнитного поля:а) безграничной плоскости, По которой течет ток с линейной плотностью $\vec{i}$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $\vec{i}$ и $- \vec{i}$, одинаковыми во всех точках каждой плоскости. Подробнее
Задача по физике — 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства. Подробнее Задача по физике — 7531
Имеется круговой виток с током $I$. Найти интеграл $\int \vec{B} d \vec{r}$ вдоль оси витка в пределах от $ — \infty$ до $+ \infty$. Объяснить полученный результат. ПодробнееЗадача по физике — 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $\vec{r}$. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $\vec{l}$. По проводу течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $\vec{l} = 0$. ПодробнееЗадача по физике — 7534
Найти плотность тока как функцию расстояния $r$ от оси аксиально-симметричного параллельного потока электронов, если, индукция магнитного поля внутри потока зависит от $r$ как $B = br^{ \alpha}$, где $b$ и $\alpha$ — положительные постоянные. ПодробнееЗадача по физике — 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$. ПодробнееЗадача по физике — 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_{0}$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $\eta = 1$%. Подробнее
Задача по физике — 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси. ПодробнееЗадача по физике — 7538
На деревянный тороид малого поперечного сечения намотано равномерно $N = 2,5 \cdot 10^{3}$ витков провода, по которому течет ток $I$. Найти отношение $\eta$ индукции магнитного поля внутри тороида к индукции магнитного поля в центре тороида. ПодробнееЗадача по физике — 7539
Постоянный ток $I = 10 А$ течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины. ПодробнееЗадача по физике — 7540
Имеется очень длинный прямой соленоид с током $I$. Площадь поперечного сечения соленоида равна $S$, число витков на единицу длины — $n$. Найти поток вектора $\vec{B}$ через торец соленоида. ПодробнееЗадачи по физике и математике с решениями и ответами
Задача по физике — 7523
Ток $I$ течет вдоль длинной тонкостенной трубы радиуса $R$, имеющей по всей длине продольную прорезь ширины $h$. Найти индукцию магнитного поля внутри трубы при условии $h \ll R$. ПодробнееЗадача по физике — 7524
Ток $I$ течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса $R$ (рис.). Найти индукцию магнитного поля в точке О.
Подробнее Задача по физике — 7525
Определить индукцию магнитного поля в точке О, если проводник с током $I$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника равен $R$, прямолинейные участки проводника предполагаются очень длинными. Подробнее Задача по физике — 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба. ПодробнееЗадача по физике — 7527
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные. Подробнее Задача по физике — 7528
Определить модуль и направление вектора $\vec{B}$ магнитного поля:а) безграничной плоскости, По которой течет ток с линейной плотностью $\vec{i}$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $\vec{i}$ и $- \vec{i}$, одинаковыми во всех точках каждой плоскости. Подробнее
Задача по физике — 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства. Подробнее Задача по физике — 7531
Имеется круговой виток с током $I$. Найти интеграл $\int \vec{B} d \vec{r}$ вдоль оси витка в пределах от $ — \infty$ до $+ \infty$. Объяснить полученный результат. ПодробнееЗадача по физике — 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $\vec{r}$. Магнитную проницаемость всюду считать равной единице. ПодробнееЗадача по физике — 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $\vec{l}$. По проводу течет постоянный ток плотности $\vec{j}$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $\vec{l} = 0$. ПодробнееЗадача по физике — 7534
Задача по физике — 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$. ПодробнееЗадача по физике — 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_{0}$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $\eta = 1$%. Подробнее
Задача по физике — 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси. ПодробнееВнутри длинного прямого провода круглого сечения имеется
Разделы 
Дополнительно
Задача по физике — 7525
Определить индукцию магнитного поля в точке О, если проводник с током $I$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника равен $R$, прямолинейные участки проводника предполагаются очень длинными.
Задача по физике — 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба.
Задача по физике — 7527
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные.
Задача по физике — 7528
Определить модуль и направление вектора $vec$ магнитного поля:
а) безграничной плоскости, По которой течет ток с линейной плотностью $vec$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $vec$ и $- vec$, одинаковыми во всех точках каждой плоскости.
Задача по физике — 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице.
Задача по физике — 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства.
Задача по физике — 7531
Имеется круговой виток с током $I$. Найти интеграл $int vec d vec$ вдоль оси витка в пределах от $ — infty$ до $+ infty$. Объяснить полученный результат.
Задача по физике — 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $vec$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $vec$. Магнитную проницаемость всюду считать равной единице.
Задача по физике — 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $vec$. По проводу течет постоянный ток плотности $vec$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $vec = 0$.
Задача по физике — 7534
Найти плотность тока как функцию расстояния $r$ от оси аксиально-симметричного параллельного потока электронов, если, индукция магнитного поля внутри потока зависит от $r$ как $B = br^< alpha>$, где $b$ и $alpha$ — положительные постоянные.
Задача по физике — 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$.
Задача по физике — 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:
а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_<0>$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $eta = 1$%.
Задача по физике — 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси.
Задача по физике — 7538
На деревянный тороид малого поперечного сечения намотано равномерно $N = 2,5 cdot 10^<3>$ витков провода, по которому течет ток $I$. Найти отношение $eta$ индукции магнитного поля внутри тороида к индукции магнитного поля в центре тороида.
Задача по физике — 7539
Постоянный ток $I = 10 А$ течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины.
Цилиндрический провод
Расчет магнитного поля чаще всего сводится к определению вектора напряженности Н. Основным законом, характеризующим свойства магнитного поля, является закон полного тока.
Рассмотрим случай по определению магнитного поля цилиндрического провода (рис.4.20).
Рис. 4.20. Схема цилиндрического провода
По прямому цилиндрическому проводу круглого сечения протекает ток I. Радиус провода a. Требуется определить напряженность магнитного поля внутри и вне провода, считая его уединенным и бесконечно длинным.
В силу симметрии линии вектора Н являются окружностями, плоскости которых перпендикулярны к оси провода. Центры этих окружностей лежат на оси цилиндра. На одинаковых расстояниях от оси цилиндра численное значение вектора Н одно и то же.
Рассмотрим линию вектора Н внутри провода. Циркуляция Нвн по этой линии равна охваченному току:
Так как Нвн вдоль контура интегрирования имеет одинаковое численное значение и направлена по касательной к линии L, то
Приравняв циркуляцию и полный ток, получим:
На поверхности проводника напряженность поля имеет наибольшее значение.
Если контур интегрирования L провести вдоль линии вектора H вне провода, циркуляция Нвш равна току в проводе:
Выражения (4.78), (4.79) позволяют определить напряженность магнитного поля в любой точке пространства как внутри провода так и вне его.
Прямой провод
Прямой провод длиной 20 см, по которому течет ток 10 А, помещен в магнитное поле под углом 30 к направлению поля. [1]
Прямой провод с электрододержателем должен быть длиной не менее половины длины секции. Обратный провод короткий, длиной около 5 м, на одном конце снабжен наконечником с отверстием для присоединения к клемме машины, а на другом — особым пружинящим контактом, плотно охватывающим трубу. [2]
Прямой провод длиной / 20 см с током / 5 А, находящийся в однородном магнитном поле с индукцией В 0 1 Тл, расположен перпендикулярно линиям магнитной индукции. [3]
Прямой провод часто называют проводом-контактом, поскольку действия криотрона напоминает работу электромагнитного реле с замкнутым контактом: если сигнал не подан на обмотку, то сопротивление прямого провода равно нулю, при подаче входного сигнала материал прямого провода выводится из области сверхпроводимости и оказывает сопротивление току. [4]
Прямой провод длиной / 10 см, по которому идет ток силой / 20 А, находится в однородном магнитном поле с индукцией В I 10 — 2 Тл. [5]
Прямой провод имеет виток радиуса R. [6]
Прямой провод длиной / 10 см находится в однородном магнитном поле с индукцией В 0 01 Тл. [7]
Прямой провод расположен между полюсами электромагнита перпендикулярно силовым линиям магнитного поля. [8]
Прямой провод имеет виток радиуса R. [9]
Прямой провод длиной 20 см, по которому течет ток 10 А, помещен в магнитное поле под углом 30 к направленно поля. [10]
Прямой провод , по которому течет ток силой / 1 кА, расположен между полюсами электромагнита перпендикулярно к линиям индукции. [11]
Прямой провод длины и направления s движется со скоростью и в магнитном поле В. Его концы соединены посредством подвижных контактов с неподвижным проводником, который вместе с ним образует замкнутую цепь. [12]
Внутри прямого провода электрическое поле повсюду одинаково. В случае 2) сумма токов, протекающих по двум параллельно соединенным проводам, равна силе тока, текущего от С к В, потому что в С никакого накопления заряда не происходит. Поэтому ток, текущий по каждому из двух параллельно соединенных проводов, равен половине силы тока на участке от С до В. Следовательно, напряженность электрического поля внутри параллельно соединенных проводов должна быть равна лишь половине напряженности электрического поля на участке между С и В. В случае 3) электрическое поле между параллельными заряженными пластинами одинаково во всех точках пространства. [13]
Внутри прямого провода круглого сечения имеется круглая цилиндрическая полость, ось которой параллельна оси провода. Смещение оси полости относительно оси провода определяется вектором а. [14]
Внутри прямого провода круглого сечения имеется круглая цилиндрическая полость, ось которой параллельна оси провода. Смещение оси полости относительно оси провода определяется вектором а. По проводу течет ток постоянной попечению плотности J. [15]
Магнитное поле цилиндрического проводника с током — Студопедия
Пусть по бесконечно длинному цилиндрическому проводу радиуса R протекает постоянный ток I . Выберем систему координат x, y, z так, чтобы ось провода совпадала с осью координат z (рис. 22).
 |
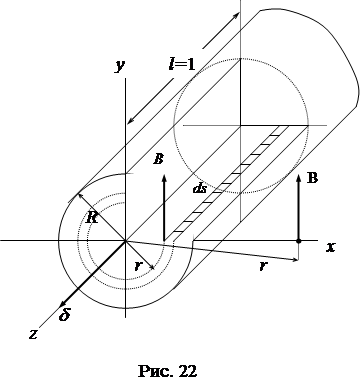Будем считать, что ток равномерно распределяется по сечению провода, тогда его плотность будет равна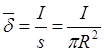 
Для исследования магнитного поля выделим две неравнозначные области, для каждой из которых выполним расчет параметров магнитного поля:
1) область внутри провода при 0 £ r £ R ,
2) область вне провода при R £ r £ ¥ .
Для расчета поля во внутренней области выберем контур интегрирования в виде окружности с текущим радиусом r<R . Тогда ток внутри контура интегрирования:
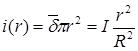, откуда 
Применим к контуру интегрирования закон полного тока в интегральной форме :
,
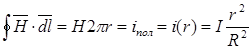откуда следует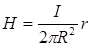 
и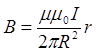 
.
Векторы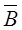 
и 
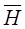направлены по касательной к окружности, их направление определяется по правилу правоходового винта.
При увеличении радиуса на элементарную величину
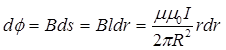
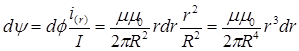
Внутренний магнитный поток и внутреннее потокосцепление найдутся в результате интегрирования полученных выше выражений по всему сечению провода:
,
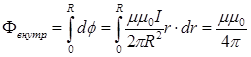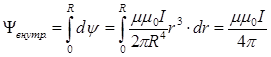
Из последнего уравнения следует формула для внутренней индуктивности провода на единицу длины :
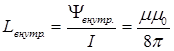[Гн/м]
Внутренняя индуктивность провода зависит от его магнитной проницаемости m (для стальных проводов она значительно больше, чем для медных или алюминиевых) и не зависит от его радиуса.
Для расчета поля во внешней области выберем контур интегрирования в виде окружности с текущим радиусом r>R . Ток внутри контура интегрирования равен I и не зависит от текущего значения радиуса
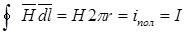, откуда 
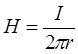и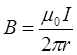 
Приращения магнитного потока dф и потокосцепления dy будут равны:
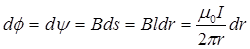
Внешний магнитный поток Фвнеш и соответственно внешнее потокосцепление Yвнеш найдутся в результате интегрирования полученных выше выражений по сечению вне провода:
,
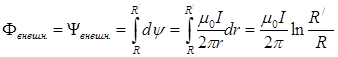где R’ < ¥ — внешний радиус в окружающем провод пространстве, где производится расчет параметров поля.
Внешняя индуктивность провода на единицу длины :
[Гн/м]
5. Магнитное поле двухпроводной линии
По двухпроводной линии с заданными геометрическими размерами (рис. 24) (R – радиус проводов, d — расстояние между осями проводов) протекает постоянный ток I.
 |
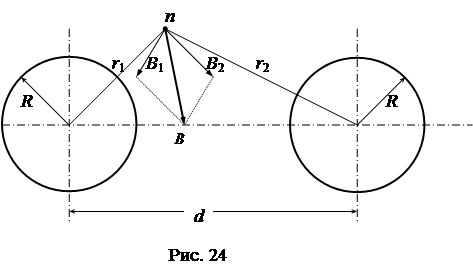Результирующий вектор магнитной индукции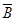 
в произвольной точке n можно определить по методу наложения как геометрическую сумму составляющих этого вектора 
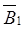и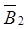 
от каждого провода в отдельности: 
=
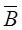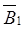
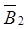. Составляющие вектора 
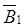и 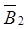определяются по полученным ранее формулам, а их направления – по правилу правоходового винта:
, 
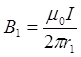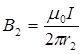
Результирующую индуктивность линии на единицу длины можно найти как сумму индуктивностей прямого и обратного провода:
L = L1 + L2 = 2Lвнут + 2L внеш = 
.
При определении внешней индуктивности провода, внешний радиус интегрирования R следует принять равным расстоянию между проводами d.
Если провода линии выполнены из неферромагнитного материала (Сu, Al) то m=1 и формула для индуктивности линии получит вид:
[ Гн / м ]
В схемах замещения трехфазных линий электропередачи учитывается индуктивность одного провода (фазы), следовательно:
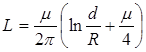[ Гн / м ] – индуктивность каждого провода (фазы) трехфазной транспонированной ЛЭП на единицу длины, где 
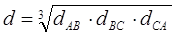– среднегеометрическое значение межосевых расстояний проводов.
Задачи по физике и математике с решениями и ответами
Задача по физике — 7555
Два длинных параллельных провода с пренебрежимо малым сопротивлением замкнуты с одного конца на некоторое сопротивление $R$, а с другого конца подключены к источнику постоянного напряжения. Расстояние между осями проводов в $\eta = 20$ раз больше радиуса сечения каждого провода. При каком значении сопротивления $R$ результирующая сила взаимодействия между проводами обратится в нуль? ПодробнееЗадача по физике — 7556
Постоянный ток $I$ течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса Л. Такой же ток течет в противоположном направлении по тонкому проводнику, расположенному на «оси» первого проводника (точка О на рис.). Найти силу магнитного взаимодействия данных проводников в расчете на единицу их длины. ПодробнееЗадача по физике — 7557
По двум длинным тонким параллельным проводникам, вид которых показан на рис., текут постоянные токи $I_{1}$ и $I_{2}$. Расстояние между проводниками $a$, ширина правого проводника $b$. Имея в виду, что оба проводника лежат в одной плоскости, найти силу магнитного взаимодействия между ними в расчете на единицу их длины.
Подробнее Задача по физике — 7558
Система состоит из двух параллельных друг другу плоскостей с токами, которые создают между плоскостями однородное магнитное поле с индукцией $B$. Вне этой области магнитное поле отсутствует. Найти магнитную силу, действующую на единицу поверхности каждой плоскости. ПодробнееЗадача по физике — 7559
Проводящую плоскость с током поместили во внешнее однородное магнитное поле. В результате индукция магнитного Поля с одной стороны плоскости оказалась $B_{1}$, а с другой стороны $B_{2}$. Найти магнитную силу, действующую на единицу поверхности плоскости в случаях, показанных на рис. Выяснить, куда направлен ток в плоскости в каждом случае.
Подробнее Задача по физике — 7560
В электромагнитном насосе для перекачки расплавленного металла участок трубы с металлом находится в однородном магнитном поле с индукцией $B$ (рис.). Через этот участок трубы в перпендикулярном к вектору $\vec{B}$ и оси трубы направлении пропускают ток $I$. Найти избыточное давление, создаваемое насосом при $\vec{B} = 0,10 Т, I = 100 А$ и $a = 2,0 см$.
Подробнее Задача по физике — 7562
Какое давление испытывает боковая поверхность длинного прямого соленоида, содержащего $n$ витков на единицу длины, когда по нему течет ток $I$? ПодробнееЗадача по физике — 7563
Ток $I$ течет по длинному однослойному соленоиду, радиус сечения которого равен $R$. Число витков на единицу длины соленоида $n$. Найти предельную силу тока, при которой может наступить разрыв обмотки, если предельная нагрузка на разрыв проволоки обмотки равна $F_{пр}$. ПодробнееЗадача по физике — 7564
Плоский конденсатор, площадь каждой пластинки которого $S$ и расстояние между ними $d$, поместили в поток проводящей жидкости с удельным сопротивлением $\rho$. Жидкость движется с постоянной скоростью $v$ параллельно пластинам. Система находится в, однородном магнитном поле с индукцией $B$, причем вектор $\vec{B}$ параллелей пластинам и перпендикулярен к направлению потока. Пластины конденсатора замкнули на внешнее сопротивление $R$. Какая мощность выделяется на этом сопротивлении? При каком значении $R$ выделяемая мощность будет максимальной? Чему равна последняя? ПодробнееЗадача по физике — 7565
Вдоль медного прямого проводника круглого сечения радиуса $R = 5,0 мм$ течет ток $I = 50 А$. Найти разность потенциалов между осью проводника и его поверхностью. Концентрация электронов проводимости у меди $n = 0,9 \cdot 10^{23} см^{-3}$. ПодробнееЗадача по физике — 7566
При измерении эффекта Холла в натриевом проводнике напряженность поперечного поля оказалась $E = 5,0 мкВ/см$ при плотности тока $j = 200 А/см^{2}$ и индукции магнитного поля $B = 1,00 Т$. Найти концентрацию электронов проводимости и ее отношение к концентрации атомов в данном проводнике. ПодробнееЗадача по физике — 7567
Найти подвижность электронов проводимости в медном проводнике, если при измерении эффекта Холла в магнитном поле с индукцией $B = 100 мТ$ напряженность поперечного электрического поля у данного проводника оказалась в $\eta = 3,1 \cdot 10^{3}$ раз меньше напряженности продольного электрического поля. ПодробнееЗадача по физике — 7568
Небольшой виток с током находится на расстоянии $r$ от длинного прямого проводника с током $I$. Магнитный момент витка равен $\vec{p}_{m}$. Найти модуль и направление вектора силы, действующей на виток, если вектор $\vec{p}_{m}$:а) параллелен прямому проводнику,
б) направлен по радиус-вектору $\vec{r}$;
в) совпадает по направлению с магнитным полем тока $I$ в месте расположения витка. Подробнее
Задача по физике — 7569
Небольшая катушка с током, имеющая магнитный момент $\vec{p}_{m}$, находится на оси кругового витка радиуса $R$, по которому течет ток $I$. Найти модуль вектора силы, действующей на катушку, если ее расстояние от центра витка равно $x$, а вектор $\vec{p}_{m}$ совпадает по направлению с осью витка. ПодробнееПлоский или круглый кабель – какой и когда лучше выбрать для проводки?
Передача электрической энергии и подключение потребителей может производиться с помощью электрокабелей как в круглом, так и в плоском исполнении. Каждый тип провода используется в различных ситуациях, условиях монтажа и эксплуатации, поэтому важно понимать, чем отличается плоский кабель от круглого для его правильного (в том числе с точки зрения экономии) применения.
В бытовом электромонтаже зачастую используют оба типа кабеля. Например, кабель марки ВВГнг существует в двух исполнениях: ВВГнг и ВВГнг-п (символ «П» в конце маркировки изделия обозначает, что он имеет плоскую форму). Такие изделия применяются при подключении стационарных электроустановок в жилых и промышленных зданиях, в том числе в сухих и сырых помещениях, а также при прокладке кабельных линий при отсутствии угрозы повреждения кабеля.
Исходя из сравнения конструктивных особенностей круглого кабеля ВВГ и его плоского варианта видно, что они отличаются:
-
Плоскостью укладки токопроводящих жил: ВВГнг-п имеет расположение жил в одной плоскости, в то время, как жилы ВВГнг уложены в параллельных друг другу плоскостях;
-
Количеством жил в общей оболочке и их сечением: у плоского кабеля из-за его конструктивных особенностей количество жил не может быть больше трех штук и каждая из них может иметь максимальное сечение 25 мм2, а вот круглого кабеля под одной общей оболочкой бывает от 1 до 5 жил и при этом сами жилы могут иметь круглое или сегментарное сечение до 500 мм2;
-
Плоские кабели не имеют защитного экрана или брони ввиду того, что защитный материал не может быть плоским и стремится к округлению.
Также два вида этих кабельных изделий различаются стойкостью к механическим воздействиям, а именно к скручиванию. Работа плоского кабеля в условиях постоянных скручивающих воздействий приводит к тому, что он будет перекручен только до определенной точки, после чего возможно повреждение жил и изоляции такого проводника. Круглый кабель может работать в условиях торсионных движений, при воздействии случайных изгибов и движения по одной оси. Плоский вариант провода может применятся в электроустановках, которые двигаются только по одной оси или являются стационарными.
Какой кабель лучше для электропроводки: плоский или круглый?
Однозначно сказать, какой электрический кабель для проводки лучше – нельзя. Применение определенного варианта связано с условиями монтажа и эксплуатации изделия. Например, при прокладке силовых магистральных линий с переменным напряжением 400 В в жилых домах и промышленных сооружениях (в специальных кабельных нишах, кабель-каналах, коробах и в скрытой проводке под полом или потолком) применяется кабель в круглом исполнении, так как имеет необходимое количество жил и большое разнообразие вариантов поперечного сечения. Такой кабель также может применятся и для электрической проводки в помещениях, он удобно протягивается в кабельные гофры и может прокладываться в них при открытой проводке.
А вот для электропроводки в помещениях часто используют кабель в плоском варианте исполнения. Это связано с удобством монтажа такого кабельного изделия в штробы в различных конструкциях (бетонных, кирпичных и прочих) и тем, что такой кабель не занимает много места в кабель-каналах и может быть скрыт за слоем отделочных материалов (штукатурки или гипсокартона). А вот использовать гофры с таки кабелем сложнее, так как требует большего поперечного сечения защитной трубки и усилий при протягивании кабеля в гофру.
Обзор марок в плоском и круглом исполнении
Производители выпускают большое количество электрических кабельных изделий в круглом и плоском исполнении. Все они выполняют различные функции и применяются при различных способах укладки, условиях эксплуатации, мощности и вида потребителей. Кратко рассмотрим некоторые из них.
Круглые кабели
NYMнг(А)-LS – круглый силовой кабель с медными жилами и негорючей ПВХ изоляцией. Имеет под общей оболочкой пониженной пожароопасности заполнение из невулканизированной резины. Предназначен для передачи электрической энергии к стационарным установкам в сетях с переменным напряжение до 0,66 кВ. Кабель выполнен по немецкой технологии и стандартам, не распространяет горение при групповой прокладке и имеет пониженное дымо- и газовыделение (Low smoke). 
АВВГ – силовой кабель в круглом исполнении, который имеет токоведущие жилы из алюминия, а изоляцию и оболочку из поливинилхлорида. Применяется для передачи электрической энергии в сетях с напряжением 0,66 и 1 кВ и подключения неподвижных потребителей бытового или промышленного назначения. Может прокладываться без ограничений по разности уровней кабельных трасс, а также на вертикальных участках.
ВБбШв – круглый силовой бронированный кабель, который имеет медные жилы, изоляцию из поливинилхлорида. Броня кабеля выполнена из стальных оцинкованных лент и не имеет подушки (под броней). Общая изоляция выполнена из выпрессованного защитного шланга. Применяется в сетях до 1 кВ для подключения стационарных электроустановок без ограничения по разности уровня по трассе прокладки.
Плоские кабели
ШВВП – плоский гибкий шнур с медной или медно-луженой жилой с изоляцией и оболочкой из ПВХ пластиката. Такое изделие применяется в сетях 220/380В для подключения светильников, бытовых приборов небольшой мощности и радиоаппаратуры, а также изготовления удлинительных шнуров для жилых зданий.
ППВ – плоский провод, который имеет разделительные перемычки между жилами. Не имеет общей изоляции для жил и может быть, как с медными жилами (ППВ), так и с алюминиевыми (АППВ). Применяется в агрессивных химических средах с переменным напряжением до 450В и частотой до 400 Гц. В сетях с постоянным напряжением используется до 1кВ. Укладывается в трубах и каналах и не подходит для гибкой укладки.
ВВГнг-LS-П – плоский кабель с медными жилами и негорючей ПВХ-изоляцией и оболочкой. Имеет пониженное дымо- и газовыделение. Применяется при передаче электрической энергии и подключении неподвижных электроустановок в сетях с напряжением 0,66 – 1 кВ.
Сила между двумя параллельными проводами
Вперед: Проблемы Up: Магнетизм Предыдущий: Соленоид
На провод № 2 будет действовать магнитное поле уравнения (1.6) из-за провод №1 предоставлен
| Б 1 = | (10) |
| знак равно | (11) |
Это хорошее упражнение, чтобы показать, что если по проводам течет ток в противоположные направления, в которых результирующие силы будут одинаковыми по величине, как в уравнении (1.11), но таковы, что вызывают отталкивание между проводами.
Эта сила между двумя токоведущими проводами вызывает фундаментальное определение Ампера:
Если два длинных параллельных провода на расстоянии 1 м друг от друга пропускают ток 1 А, тогда сила на единицу длины на каждом проводе равна 2 x 10 — 7 Н / м.Это определение Ампера затем приводит к основному определению единицы заряда кулон:
Провод с током 1 А проходит через заданную точку на 1 ° C. заряда в секунду.Это определение также объясняет причину, по которой константа уравнения.(1.7) было дано в точности так как 4 x 10 — 7 Т м / А.
Вперед: Проблемы Up: Магнетизм Предыдущий: Соленоид www-admin@theory.uwinnipeg.ca
09.10.1997 .
Phys 202 заключительные карточки — Cram.com
Нам не удалось определить язык звукового сопровождения на ваших карточках. Пожалуйста, выберите правильный язык ниже.
Фронт Китайский (пиньинь) Китайский упрощенный Китайский традиционный английский французский язык Немецкий Итальянский японский язык Японский, ромадзи корейский язык Математика / символы русский испанский африкаанс Акан Аккадский албанский Амхарский арабский Армянский Азербайджанский Баскский Белорусский Бенгальский Бихари Бретонский болгарский Бирманский Каталонский Себуано Чаморро Химия Чероки Китайский (пиньинь) Китайский упрощенный Китайский традиционный Чокто Коптский Корсиканский хорватский Чешский Датский Дене Дивехи нидерландский язык английский эсперанто эстонский Фарерские острова Филиппинский Финский французский язык Фула Гэльский Галицкий Грузинский Немецкий Греческий Гуарани Гуджарати Хайда Гаитянский Хауса Гавайский иврит хинди венгерский язык исландский Игбо индонезийский Инуктитут Ирландский Итальянский японский язык Японский, ромадзи Яванский Каннада Казахский Кхмерский корейский язык Курдский Кыргызский Лакота Лаосский латинский Латышский Лингала Литовский Люба-Касаи Люксембургский македонский малайский Малаялам Мальтийский маори Маратхи Маршалльский Математика / символы Монгольский Непальский Норвежский Окситанский Оджибве Ория Оромо Другое / Неизвестно Пушту Персидский Польский португальский Пенджаби Пали кечуа румынский Ретороманский русский санскрит сербский Синдхи Сингальский словацкий словенский испанский Суданский суахили Шведский Тагальский Таджикский Тамильский Татарский телугу Тайский тибетский Тигринья Тохоно О’одхам Тонга турецкий Уйгурский украинец Урду Узбекский вьетнамский валлийский Западно-фризский идиш Йорубааудио еще не доступно для этого языка
Назад Китайский (пиньинь) Китайский упрощенный Китайский традиционный английский французский язык Немецкий Итальянский японский язык Японский, ромадзи корейский язык Математика / символы русский испанский африкаанс Акан Аккадский албанский Амхарский арабский Армянский Азербайджанский Баскский Белорусский Бенгальский Бихари Бретонский болгарский Бирманский Каталонский Себуано Чаморро Химия Чероки Китайский (пиньинь) Китайский упрощенный Китайский традиционный Чокто Коптский Корсиканский хорватский Чешский Датский Дене Дивехи нидерландский язык английский эсперанто эстонский Фарерские острова Филиппинский Финский французский язык Фула Гэльский Галицкий Грузинский Немецкий Греческий Гуарани Гуджарати Хайда Гаитянский Хауса Гавайский иврит хинди венгерский язык исландский Игбо индонезийский Инуктитут Ирландский Итальянский японский язык Японский, ромадзи Яванский Каннада Казахский
.ПРЯМОЙ ПРОВОД — АУДИО СОЕДИНЕНИЯ: аудиокабели, видеокабели, разъемы, HDMI, кабель домашнего кинотеатра
| ||||||||||
| ||||||||||
Уровень 1: существенное обновление кабелей, поставляемых производителем | ||||||||||
| Musicable II IC является фаворитом для раскрытия потенциала цифровых ресиверов объемного звука, DVD- и CD-плееров, музыкальных серверов, MP3-плееров, DVR, сабвуферов и других компонентов.Его усовершенствованная полипропиленовая изоляция и сбалансированный дизайн Star Quad подчеркивают глубину и тонкость ваших любимых записей. Двойные экраны отлично подавляют шум при длительных пробежках. XLR (симметричная заделка) Матовая темно-синяя куртка | |||||||||
| Chorus AG IC раскрывает детали ваших любимых фильмов и музыки, чтобы улучшить ваши домашние развлечения.Изоляция из спеченного пенопласта из PTFE и посеребренные проводники из бескислородной меди (OFC) создают великолепный звуковой реализм и глубину. Chorus AG использует усовершенствованную симметричную коаксиальную конструкцию для обеспечения бескомпромиссного сигнала, включая мельчайшие детали и плотные, точные басы. Он уловит и высвободит все тонкости, которые вам нравится слышать. | |||||||||
Уровень 2: Значительное улучшение качества звука по сравнению со стандартными кабелями | ||||||||||
| Symphony II IC расширяет презентационные возможности лучшей электроники.Его шелковистые средние частоты и богатые расширенные возможности извлечения басов передают всю естественную текстуру вокала и инструментов. Он включает специальную изоляцию из пенопласта TPR вокруг групп медных проводников OFHC в сбалансированной конструкции Star Quad. Отлично подходит для интегрированных усилителей среднего уровня, компонентов с дискретной аналоговой аудиосистемой, лучших сабвуферов и лучшего цифрового оборудования! XLR (симметричная заделка) и телескопическая заделка | |||||||||
| Encore II IC использует проводники OFHC с изоляцией из пенополипропилена высшего качества для неокрашенной презентации с захватывающим вокалом.Самый продвинутый дизайн Star-Quad от Straight Wire, Encore II, обеспечивает реалистичные плотные басы и истинные верхние частоты независимо от длины кабеля. Высокая совместимость этого кабеля практически со всеми компонентами делает его очевидным выбором среди конкурентов. Откройте для себя значительные улучшения, которые Encore II может сделать с помощью современных цифровых приемников и большинства отдельных компонентов. Прозрачная куртка поверх красной тесьмы — Международный журнал Audio Video | |||||||||
Уровень 3: Кабели для аудиофилов с высоким уровнем артикуляции | ||||||||||
| Rhapsody S IC был разработан на основе винтовой конструкции с низким сопротивлением, использующей шесть групп проводников. Медь OFHC с серебряным покрытием обеспечивает детальную артикуляцию всех частот с роскошной музыкальностью.Изоляция из пенополипропилена изолирует каждую группу в среде с низкой диэлектрической проницаемостью. Вы войдете в голографическую звуковую сцену, как в исходное место записи. Подтвержденный отбор квалифицированного отраслевого персонала для проведения торговых выставок. XLR (симметричная заделка) Прозрачная куртка поверх синей тесьмы | |||||||||
| Expressivo IC включает технологию сжатых проводов Воздушное пространство и звуковая сцена замечательно определены с быстрым и точным темпом. Частоты верхнего регистра имеют соответствующую скорость и тембр с четкой гармонической структурой. Отрывки среднего уровня предлагают естественное шипение и эмоциональный характер, что приближает вас к вашим любимым записям.Средние басы плотные с соответствующим затуханием, в то время как нижние регистры полны мощи и истинного воздействия. XLR (симметричная заделка) и телескопическая заделка Сетчатая куртка поверх синей тесьмы | |||||||||
| Serenade II IC использует сертифицированные медные проводники CDA 101 в усовершенствованной конструкции Helix CCT (технология сжатых проводников) с низким сопротивлением.Он передает музыкальную структуру и динамические отрывки с большой фокусировкой и ясностью. В этом «младшем брате», удостоенном наград Crescendo, средние басы и когерентность среднечастотных частот повышены. Он очаровывает слушателя легкой передачей исходного воздушного пространства и деталей. Неограниченная производительность. безупречные высокие частоты, великолепный средний диапазон и мощные басы очевидны при использовании вместе с аудиокомпонентами высокого уровня. Serenade II передает все нюансы ваших любимых исходных материалов. XLR (симметричная заделка) | |||||||||
Уровень 4: Кабели эталонного качества | ||||||||||
Эти кабели не для случайного слушателя, в них используется супер-микропористая изоляция из пенопласта PTFE и высококачественные фиксирующие разъемы из золота / PTFE для высокой скорости распространения и наилучшего соединения.Уникальные проводники CCT обеспечивают скорость, четкость и басы, недостижимые для других кабелей. | ||||||||||
| Virtuoso R2: поражает захватывающим балансом артикуляции и реалистичной музыкальной подачи с выдающейся связностью и динамикой. Многие из самых уважаемых в мире производителей аудиофилов полагаются на межблочные кабели Virtuoso для окончательного «озвучивания» своих эталонных систем. Мы надеемся, что вы тоже будете доверять Virtuoso в своей справочной системе.Он одинаково хорошо работает как в твердотельных, так и в ламповых системах. XLR (симметричная заделка) и телескопическая заделка Прозрачный жакет поверх черной / серой тесьмы; | |||||||||
| Crescendo 3: радикально отличается от всех существующих конструкций межсоединений.Ни в одном другом кабеле с прямым проводом не использовались расширенные полевые испытания и отзывы дилеров, а также такие мелкие доработки. Благодаря усовершенствованному массиву спиралей, состоящему из множества групп проводников, он имеет самое низкое сопротивление среди всех межсоединений. Устранены все динамические ограничения; Остающийся — это наиболее голографически правдоподобный звуковой ландшафт, способный перенести слушателя в исходное пространство записи. С Crescendo музыка более чем увлекает слушателя. Вы будете различать каждого музыканта и его инструмент.Без малейшего намека на зернистость или блики вы уловите каждую мелочь, что позволит вам слышать все место выступления. Этот компонент предназначен для немногих избранных, у которых есть ресурсы и среда, чтобы по-настоящему оценить такой кабель. XLR (симметричная заделка) и телескопическая заделка (привяжите экран к заземлению на одном конце) доступны вместе со стандартной заделкой RCA Прозрачный жакет поверх черной / серой тесьмы; Диаметр 19 мм (..740 «) | |||||||||
| Вернуться к межсоединениям | ||||||||||
| ВНУТРЕННИЙ КАБЕЛЬ для индивидуальных и домашних работ. | ||||||||||
| Инновационные кабели и вилки «Push-Prong» были разработаны Стивеном Хиллом, президентом компании Straight Wire, с учетом растущего спроса на заделку нестандартных кабелей в полевых условиях, быстро и без припоя.Большинство компрессионных пробок не подлежат повторному использованию, поэтому, если установщик допустит ошибку, они должны отрезать пробку и выбросить ее. Заглушки «Push-Prong» с прямым проводом можно использовать повторно, просто отвинтив цилиндр и отогнув штыри, чтобы удалить кабель, отрезать его по длине и снова заделать. Вилки предназначены для наилучшей работы с любым коаксиальным кабелем с одножильным проводом 23 AWG — отраслевым стандартом вещания. Straight Wire предлагает полную линейку посеребренных коаксиальных кабелей 23 калибра премиум-класса — одинарные, двойные (сиамские), тройные (параллельные) и их победившую серию Silver под круглой оболочкой, включая 2, 3, 5 и 5 коаксиальных кабелей с двумя кабелями Cat5E | | |||||||||
КАБЕЛИ С ПУЛЬТОМ | ||||||||||
Серебро 23 — Одиночный, Коаксиальный провод с серебряным покрытием 23 калибра, изоляция белого цвета Серебро 23 — двойной, «Сиамский» коаксиальный кабель 23 калибра, посеребренный, изоляция красного и белого цветов | | |||||||||
Провода 23 калибра в одинарной круглой оболочке | ||||||||||
Silver 5 PLUS: Пять (5) мини-коаксиальных кабелей 75 Ом с покрытием Silver 5: Пять (5) мини-коаксиалов сопротивлением 75 Ом с посеребренными центральными проводниками Серебристый 3: Три (3) мини-коаксиальных кабеля на 75 Ом с посеребренными центральными проводниками Silver 2: Два (2) мини-коаксиальных кабеля на 75 Ом с посеребренными центральными проводниками | ||||||||||
| ||||||||||
Межблочные соединения сабвуфера обеспечивают передачу сигналов низкого уровня на питание сабвуферы (со встроенными усилителями).Они в первую очередь подключены к выходам LFE AV-ресиверы или предусилители с одиночным или двойное соединение со стороны нагрузки. Проконсультируйтесь со знающим AV специалист о преимуществах двойного подключения по дизайну вашего сабвуфера (ов). Несколько сабвуферов предназначены для подключения к полному диапазону левый / правый выходы предусилителя (если есть) для лучшей производительности с полным диапазоном сигнала.Будьте осторожны при использовании Y-кабеля в источник и длинные сабвуфера работают, что может ухудшить выход предусилителя качество основных каналов усилителя. Некоторые сабвуферы лучше работают с высокими уровень входов через акустический кабель от внешних усилителей. Если вы этого не сделаете у вас есть знающий советник по AV — свяжитесь с нами, чтобы помочь вам выберите лучший кабель для сабвуфера для вашей системы. Все эти кабели имеют усовершенствованную геометрию Star Quad с
различная изоляция и проводники. Все кабели для сабвуфера Straight Wire
оканчивается в стандартном формате для низкого сопротивления и даже экранного шума
распространение. По запросу они могут быть оконцованы в сбалансированном формате (XLR) и в одностороннем соединении экрана. | ||||||||||
| MUSICABLE (MCASUB) — хороший выбор | |||||||||
Matte Grey Jacket 
Темно-серая куртка 
XLR (симметричная заделка) и телескопическая заделка 
